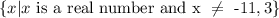Question

Let f(x) = 3/3-× and g (×) = 11+x find the domain of (f/g) (x)

Answer 1

`\lbrace x|x\text{ is a real number and x }\\e\text{ -11},3\rbrace`

Step-by-step explanation:

Here, we want to get the domain of the given function

We start by dividing the two as follows:

`((f)/(g))(x)\text{ = }(f(x))/(g(x))`
`\begin{gathered} So,\text{ we have it that:} \\ (3)/(3-x)*(1)/(11+x)\text{ = }(3)/(33+3x-11x-x^2)\text{ = }(3)/(33-8x-x^2) \end{gathered}`

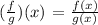
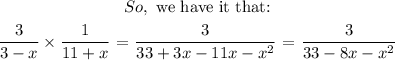
The domain refers to the possible x-values

To get that, we need to solve the quadratic equation in the denominator

We have that as:

`\begin{gathered} 33-8x-x^2=0 \\ 33-11x+3x-x^2=0 \\ 11(3-x)+x(3-x)=\text{ 0} \\ (11+x)(3-x)\text{ = 0} \\ x\text{ = -11 or 3} \end{gathered}`

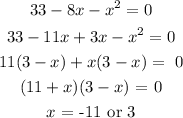
So, we have the domain as:

`\mleft\lbrace x|x\text{ is a real number and x }\\e\text{ -11},3\mright\rbrace`