We are given the following infinite geometric series
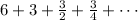
The general form of an infinite geometric series is given by
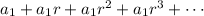
Where a1 is the first term and r is the common ratio.
The first term is equal to 6
The common ratio is the division of any two consecutive numbers in the infinite geometric series.
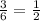
You can also take any other two consecutive numbers in the series and you will get the same common ratio.
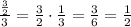
As expected, we still got the same common ratio as before.
How do I find out whether an infinite geometric series converges?
An infinite geometric series converges if the absolute value of the common ratio is less than 1.
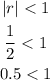
Since the absolute value of the common ratio is less than 1, the infinite geometric series converges.
How do I find its sum?
The sum of this infinite geometric series is given by
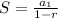
Substitute the values of first term a1 and common ratio r.
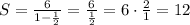
Therefore, the sum of this infinite geometric series is 12.