Question

A bicycle wheel, of radius 0.300 m and mass 2.07 kg (concentrated on the rim), is rotating at 4.00 rev/s. After 59.0 s the wheel comes to a stop because of friction. What is the magnitude of the average torque due to frictional forces?

Answer 1

0.079 J

Explanation:

The average torque exerted due to friction force is:

`\tau=I\alpha`

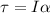
Here, I is the moment of inertia and α is the angular acceleration.

The mass of wheel is concentrated at the rim. Therefore, the moment of inertia of wheel is,

`I=m\cdot r^2`

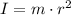
Here, m is the mass of wheel and r is the radius of wheel.

replacing:

`\begin{gathered} I=2.07\cdot0.3^2 \\ I=0.1863\text{ kg}\cdot s^2 \end{gathered}`

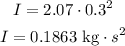
The angular speed is decreased from 4 rev/s to 0 rev/s in 59 sec. Therefore, the angular acceleration is calculated as:

`\begin{gathered} \alpha=(0-4)/(59) \\ \alpha=0.068\cdot(rev)/(\sec)\cdot\frac{2\pi\text{ rad/rev}}{1rev/sec^2} \\ \alpha=-0.426rad/sec^2 \end{gathered}`

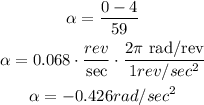
The negative sign represents that the wheel is de-accelerating.

Replacing:

`\begin{gathered} \tau=I\alpha \\ \tau=0.1863\cdot-0.426 \\ \tau=-0.079\text{J} \end{gathered}`

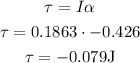
The negative sign represents the direction of torque i.e. clockwise direction. Thus, the magnitude of average torque is 0.079 J.