Given a general quadratic expression:

firs, lets divide both sides of the equation by 'a' :
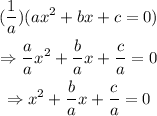
next, we can move the term c/a to the right side of the equation:
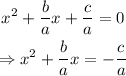
now we are ready to complete the square on the left side. What we have to do, is to take the constant that is multiplying x (in this case,b/a), and first, we divide it by 2, and then elevate to the square the result:
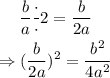
then, adding this number on both sides of the equation, we get:
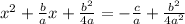
which we can write like this:
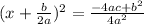
applying the square root on both sides,we get the following:
![\begin{gathered} \sqrt[]{(x+(b)/(2a))^2}=\sqrt[]{(b^2-4ac)/(4a^2)}=\pm\frac{\sqrt[]{b^2_{}-4ac}}{2a} \\ \Rightarrow x+(b)/(2a)=\pm\frac{\sqrt[]{b^2-4ac}}{2a} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/bvby3yw6nk4xj26swot79dtfeis0a9rncb.png)
finally, we can solve for x:
![\begin{gathered} x+(b)/(2a)=\pm\frac{\sqrt[]{b^2-4ac}}{2a} \\ \Rightarrow x=-(b)/(2a)\pm\frac{\sqrt[]{b^2-4ac}}{2a}=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/iut5nxbiht4tu9z19o6r9bv41d9oaw703c.png)
as we can see, if we have a general quadratic equation, we can us the completing the square method to deduce the quadratic formula