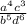Question

How does a to the 4 b to -5 over c to -3 d to the 6th get simplified?

Answer 1

Given the expression

`(a^4b^(-5))/(c^(-3)d^6)`

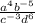
To simplify the expression above, we convert all negative indices to positive indices

Applying the rule of indices

`a^(-x)=(1)/(a^x)`

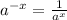
Applying the rule to the given expression gives

`\begin{gathered} \text{Where b}^(-5)=(1)/(b^5)\text{ and} \\ c^(-3)=(1)/(c^3) \end{gathered}`

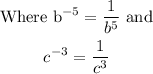
Substitute the above deduction into the given expression

`\begin{gathered} (a^4b^(-5))/(c^(-3)d^6)=a^4*(1)/(b^5)*(1)/((1)/(c^3))*(1)/(d^6) \\ \text{Where }(1)/((1)/(c^3))=c^3 \\ =a^4*(1)/(b^5)*(1)/((1)/(c^3))*(1)/(d^6)=a^4*(1)/(b^5)* c^3*(1)/(d^6) \\ =(a^4c^3)/(b^5d^6) \\ (a^4b^(-5))/(c^(-3)d^6)=(a^4c^3)/(b^5d^6) \end{gathered}`

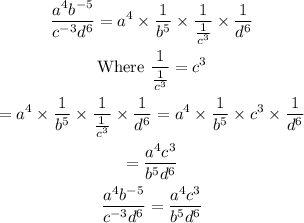
Hence, the simplified form is

`(a^4c^3)/(b^5d^6)`