The given equations of the lines are in their slope-intercept form, that is:
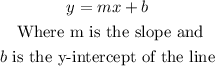
Then, we have:
• First equation
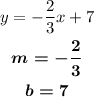
• Second equation

Now, to graph the first equation, we can find two points through which the line passes:
• First point
If x = 3, then we have:
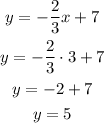
That means that the line passes through the point (3,5).
• Second point
If x = 6, then we have:
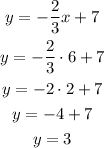
That means that the line passes through the point (6,3).
To graph the second equation, we can find two points through which the line passes:
• First point
If x = 3, then we have:
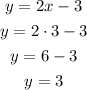
That means that the line passes through the point (3,3).
• Second point
If x = 4, then we have:
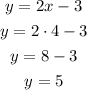
That means that the line passes through the point (4,5).
Now that we know two points through which each line passes, we can graph them and then join them to obtain the graph of both equations: