Given:
a1 = 4
a3 = 1
r = ½
Let's find the S3 of the sum of the geometric series.
Apply the sum of geometric series formula below:
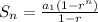
Let's solve for S3.
Substitute the values into the equation.
Where: n = 3
Thus, we have:
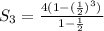
Solving further:

Therefore, the S3 of the sum of the given geometric series is 7
ANSWER:
7