Given: An objective function
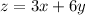
with constraints-
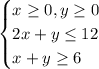
Required: To graph the linear inequalities representing the constraints and determine the objective function's value at each corner.
Explanation: The inequalities can be graphed by considering them as equations and then determining the shaded region by less than or greater than symbol.
The equation for the first inequality is-
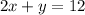
This represents a straight line passing through points (6,0) and (0,12).
The shaded region will be below this line as the inequality is-
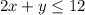
Similarly, the inequality-
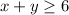
Represents a shaded region above the line x+y=6.
The inequalities-
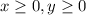
Represents the positive values of x and y. Hence we need to determine the graph in the first quadrant.
The graph of the inequalities is-
The graph in blue represents the inequality-
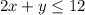
While the graph in green represents the inequality-
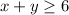
The corner points of the common shaded area are A(0,6), B(0,12), and C(6,0).
Now the value of the objective function at these points is-
a) At A(0,6)
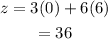
b) At B(0,12)
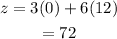
c) At C(6,0)

Final Answer: a) The graph is drawn.
b) 36,72,18