Question

If a ball is thrown with an initial horizontal velocity of 2.3m/s, from a tall building, how far away from thebuilding does the ball land if it takes 4s to land?Referring to the ball above, how tall is the building? (2 sig figs)

Answer 1

Given,

The initial velocity of the ball, u=2.3 m/s

The time interval in which the ball hits the ground, t=4 s

As the ball was thrown horizontally, the angle of projection is θ=0°

The distance traveled by the ball in the horizontal direction is given by,

`\begin{gathered} x=u_xt \\ \Rightarrow x=u\cos \theta* t \end{gathered}`

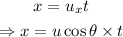
Where uₓ is the x-component of the initial velocity.

On substituting the known values,

`\begin{gathered} x=2.3*\cos 0^(\circ)*4 \\ =9.2\text{ m} \end{gathered}`

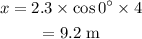
Therefore the distance traveled by the ball in the x-direction is 9.2 m. That is the ball landed 9.2 meters away from the building.

Applying the equation of the motion in the y-direction,

`\begin{gathered} y=y_0+u_yt+(1)/(2)gt^2 \\ =y_0+u\sin \theta*_{}t+(1)/(2)gt^2 \end{gathered}`

Where y is the final height of the ball which is zero meters, y₀ is the initial height of the ball, i.e., the height of the building, uy is the y-component of the initial velocity.

Let us consider that the upward direction is positive while the downward direction is negative. This makes the acceleration due to gravity, g, a negative value, and the height of the building a positive value.

On substituting the known values,

`\begin{gathered} 0=y_0+2.3*\sin (0^(\circ))*4+(1)/(2)*-9.8*4^2 \\ \Rightarrow-y_0=0-4.9*4^2 \\ y_0=78.4\text{ m} \\ \approx78\text{ m} \end{gathered}`

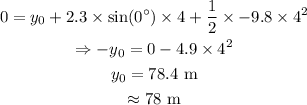
Therefore the height of the building is 78 m