a) Doubling time of the population.
Initial population = 4
Doubling = 2 x 4 = 8
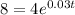
Then, solve for t:
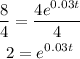
Apply the exponent laws:
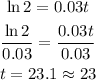
Answer a: 23 years
b) Initial population = 4
Triple the population = 3 x 4 = 12
Therefore:
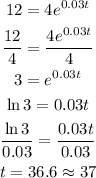
Answer b: 37 years
c) Initial population = 4
Quadruple the population = 4 x 4 = 16
So:
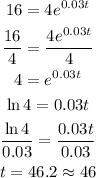
Answer c: 46 years