Question

A firm has a monthly fixed cost of $2000, and the variable cost per unit of its product is $25. a. Determine the cost function. b. The revenue R obtained by selling x units is given by R(x) = 60x - 0.01x2. Determine the number of units that must be sold each month so as to maximize the revenue. What is the maximum revenue? c. How many units must be produced and sold each month to obtain a maximum profit? What is the maximum profit?

Answer 1

a) We can write the cost function (in function of the units made) as the sum of the fixed cost (2000) and the variable cost (25*x):

`C(x)=2000+25x`

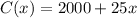
b) The revenue R(x) is:

`R(x)=60x-0.01x^2`

To find the value of x that maximizes R(x) we derive R(x) and equal it to 0:

`(dR)/(dx)=60(1)-0.01(2x)=60-0.02x`
`\begin{gathered} (dR)/(dx)=0 \\ 60-0.02x=0 \\ 60=0.02x \\ x=(60)/(0.02) \\ x=3000 \end{gathered}`

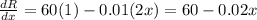
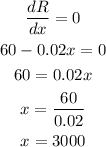
We can now calculate the maximum revenue as R(3000):

`\begin{gathered} R(3000)=60\cdot3000-0.01\cdot(3000)^2 \\ R(3000)=180000-0.01\cdot9000000 \\ R(3000)=180000-90000 \\ R(3000)=90000 \end{gathered}`

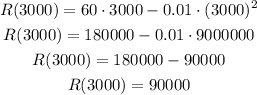
c) The profit function P(x) can be calculated as the difference between the revenue and the cost:

`\begin{gathered} P(x)=R(x)-C(x) \\ P(x)=(60x-0.01x^2)-(2000+25x) \\ P(x)=-0.01x^2+60x-25x-2000 \\ P(x)=-0.01x^2+35x-2000 \end{gathered}`

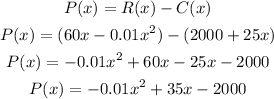
In the same way as we did in b), we can calculate the number of units x that maximize the profit by deriving P(x) and making it equal to 0:

`\begin{gathered} (dP)/(dx)=-0.01(2x)+35(1)-2000(0)=0 \\ -0.02x+35=0 \\ 35=0.02x \\ x=(35)/(0.02) \\ x=1750 \end{gathered}`

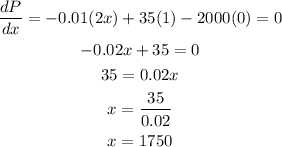
The maximum profit can be then calculated as P(1750):

`\begin{gathered} P(1750)=-0.01(1750)^2+35(1750)-2000 \\ P(1750)=-0.01\cdot3062500+61250-2000 \\ P(1750)=-30625+61250-2000 \\ P(1750)=28625 \end{gathered}`

We can graph R(x) and P(x) as:

Answer:

a) C(x) = 2000 + 25x

b) x = 3000 units

R(3000) = $90000

c) x = 1750 units

P(1750) = $28625