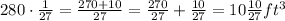First, we need to convert the mixed numbers into fractions

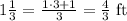
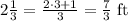
To find how many cubes fit on the length, we need to divide 10/3 by 1/3, as follows:

To find how many cubes fit on the width, we need to divide 4/3 by 1/3, as follows:
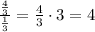
To find how many cubes fit on the height, we need to divide 7/3 by 1/3, as follows:
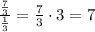
Then, the length has 10 cubes, the width has 4 cubes, and the height has 7 cubes.
The volume of each cube is:
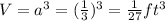
The number of cubes that fit in the rectangular prism is: 10x4x7 = 280. Therefore, the volume of the prism is