Question

Given: ∠D ≅ ∠C and ∠CAB ≅ ∠DBA. Prove ΔABC ≅ ΔBAD

Answer 1

To prove that

`\Delta ABC\cong\Delta BAD`

We have to prove that they share at least 2 angles.

1.

`\angle D\cong\angle C`

This is a given fact.

2.

Notice that

`\Delta ADE\cong\Delta\text{BEC}`

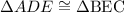
Since they already share two angles: DEA and CEB (They are vertically opposite)

This way, we can conclude that:

`\angle DAE\cong\angle\text{CBE}`

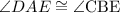
In other words, the two angles on top of A and B are equal.

Therefore, we can conclude that

`\angle DAB\cong\angle CBA`

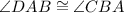
And since ΔABC and ΔBAD share two of their angles, we can conclude that they also share their third and that:

`\Delta ABC\cong\Delta BAD`

Q.E.D