Question

use the given conditions to write an equation for each line in the point-slope form and slope-intercept form (-3,2) with slope -6

Answer 1

`y=-6x-16`

Step-by-step explanation

the slope-intercept form of a line has the form:

`\begin{gathered} y=mx+b \\ where\text{ m is the slope} \\ and\text{ b is the y-intercept} \end{gathered}`

when given the slope and a point of the line we can use the slope-point formula, it says.

`\begin{gathered} y-y_1=m(x-x_1) \\ where\text{ m is the slope} \\ (x_1,y_1)\text{ is a point of the line} \end{gathered}`

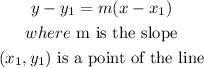
so

Step 1

a)Let

`\begin{gathered} slope=\text{ -6} \\ point\text{ \lparen -3,2\rparen} \end{gathered}`

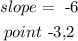
b) now, replace and solve for y

`\begin{gathered} y-y_(1)=m(x-x_(1)) \\ y-2=-6(x-(-3)) \\ y-2=-6(x+3) \\ y-2=-6x-18 \\ add\text{ 2 in both sides} \\ y-2+2=-6x-18+2 \\ y=-6x-16 \end{gathered}`

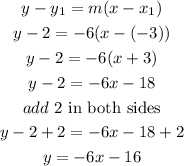
so, the equation of the line is

`y=-6x-16`

I hope this helps you