Given:
The minimum of a parabola is located at (–1, –3).
The general equation of the parabola will be as follows:

Where (h,k) is the vertex of the parabola
given the vertex is the minimum point (-1, -3)
So, h = -1, k = -3
substitute into the general form, so, the equation of the parabola will be:
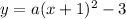
The point (0, 1) is also on the graph.
So, when x = 0, y = 1
substitute with the given point to determine the value of (a)
So, the equation will be:
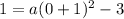
So, the answer will be the first option:
1 = a(0 + 1)^2 – 3