Question

There is a population of 2,363 bacteria in a colony. If the number of bacteria doubles every 157 minutes, what will the population be 314 minutes from now?

Answer 1

9452

Step-by-step explanation

an exponential function is given by:

`\begin{gathered} y=a(b)^x \\ \text{where a is the initial amount} \\ b\text{ is the rate of change} \\ x\text{ is the time} \end{gathered}`

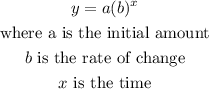
so

Step 1

Set the equations

a) initial population = 2363

time=0

replace

`\begin{gathered} y=a(b)^x \\ 2363=a(b^0) \\ 2363=a\cdot1 \\ 2363=a \end{gathered}`

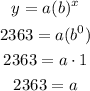
b) If the number of bacteria doubles every 157 minutes

`\begin{gathered} (2363\cdot2)=2363(b^(157)) \\ (2363\cdot2)=2363(b^(157)) \\ 4726=2363b^(157) \\ \text{divide both sides by }2363 \\ (4726)/(2363)=(2363b^(157))/(2363) \\ 2=b^(157) \\ 2^{((1)/(157))}=(b^(157))^{(1)/(157)} \\ 1.00442471045\text{ =b} \end{gathered}`

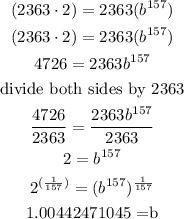
so, the function is

`y=2363(1.00442471045)^x`

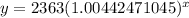
Step 2

what will the population be 314 minutes from now?

Let

time=x =314

replace

`\begin{gathered} y=2363(1.00442471045)^x \\ y=2363(1.00442471045)^(314) \\ y=2363\cdot4 \\ y=9452 \end{gathered}`

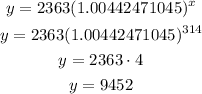
therefore, the answer is

9452

I hope this helps you