Given in triangle ABC , m∠A = 75°, m∠B = 65°, a = 23.5ft.
We have to find the third angle,

The shortest angle is angle C. So, the shortest side will be opposite to angle C.
Use the sine rule, to find the third side as follows:
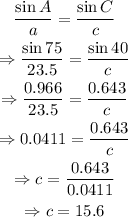
Thus. the length of the shortest side is 15.6 ft.