We are asked to determine the force that the tractors is exerting on a trailer up an incline. A free-body diagram of the situation is the following:
Where:

Now, we add the forces in the direction of the incline:
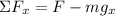
To determine the x-component of "mg" we use the following right triangle:
Now, we use the function sine to determine the value of "mgx":
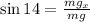
Now, we multiply both sides by "mg":
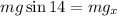
Now, we substitute the values of "m" and "g":
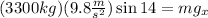
Solving the operations:
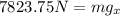
Now, we substitute the value in the sum of forces:
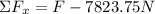
Since the object is moving at a steady speed this means that the sum of forces is zero:
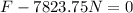
Now, we add 7823.75N to both sides:
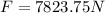
Therefore, the tractor exerts a force of 7823.75N