Question

Volume of the box with the cone shape cut out of it. What are the side lengths of the box and what is the volume of the box/cube only?

Answer 1

Side length of the box: 6 cm

Volume of the box/cube: 216 cm³

Volume of the box without cone: 190.88 cm³

Step-by-step explanation:

The sides of a cube are all equal, so in this case, the side length of the box is 6 cm.

Then, the volume can be calculated as

Volume = side x side x side

Volume = 6 cm x 6 cm x 6 cm

Volume = 216 cm³

To know the volume of the box with the cone shape cut of it, we need to calculate the volume of the cone with the following equation

`Volume=(1)/(3)\pi r^2h`

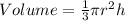
Where π = 3.14, r is the radius and h is the height. The diameter of the cone is 4 cm, so the radius is

r = 4 cm/2 = 2 cm

Then, replacing r = 2 cm and h = 6 cm, we get

`\begin{gathered} Volume=(1)/(3)(3.14)(2\text{ cm\rparen}^2(6\text{ cm\rparen} \\ Volume=(1)/(3)(3.14)(4\text{ cm}^2)(6\text{ cm\rparen} \\ Volume=25.12\text{ cm}^3 \end{gathered}`

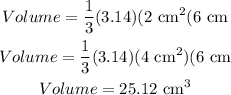
Now, the volume of the box without the cone shape is

V = 216 cm³ - 25.12 cm³

V = 190.88 cm³

So, the answers are

Side length of the box: 6 cm

Volume of the box/cube: 216 cm³

Volume of the box without cone: 190.88 cm³