Question

Solving a trigonometric equation involving an angle multiplied by a constant

Answer 1

In these questions, we need to follow the steps:

1 - solve for the trigonometric function

2 - Use the unit circle or a calculator to find which angles between 0 and 2π gives that results.

3 - Complete these angles with the complete round repetition, by adding

`2k\pi,k\in\Z`

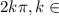
4 - these solutions are equal to the part inside the trigonometric function, so equalize the part inside with the expression and solve for x to get the solutions.

1 - To solve, we just use algebraic operations:

`\begin{gathered} \sqrt[]{3}\tan (3x)+1=0 \\ \sqrt[]{3}\tan (3x)=-1 \\ \tan (3x)=-\frac{1}{\sqrt[]{3}} \\ \tan (3x)=-\frac{\sqrt[]{3}}{3} \end{gathered}`

2 - From the unit circle, we can see that we will have one solution from the 2nd quadrant and one from the 4th quadrant:

The value for the angle that give positive

`+\frac{\sqrt[]{3}}{3}`

is known to be 30°, which is the same as π/6, so by symmetry, we can see that the angles that have a tangent of

`-\frac{\sqrt[]{3}}{3}`

Are:

`\begin{gathered} \theta_1=\pi-(\pi)/(6)=(5\pi)/(6) \\ \theta_2=2\pi-(\pi)/(6)=(11\pi)/(6) \end{gathered}`

3 - to consider all the solutions, we need to consider the possibility of more turn around the unit circle, so:

`\begin{gathered} \theta=(5\pi)/(6)+2k\pi,k\in\Z \\ or \\ \theta=(11\pi)/(6)+2k\pi,k\in\Z \end{gathered}`

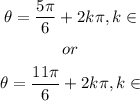
Since 5π/6 and 11π/6 are π radians apart, we can put them together into one expression:

`\theta=(5\pi)/(6)+k\pi,k\in\Z`

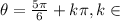
4 - Now, we need to solve for x, because these solutions are for all the interior of the tangent function, so:

`\begin{gathered} 3x=\theta \\ 3x=(5\pi)/(6)+k\pi,k\in\Z \\ x=(5\pi)/(18)+(k\pi)/(3),k\in\Z \end{gathered}`

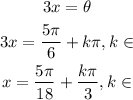
So, the solutions are:

`x=(5\pi)/(18)+(k\pi)/(3),k\in\Z`