Given data:
* The area of the parallel plate capacitor is,
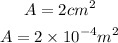
* The distance between the plates is,
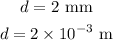
Solution:
(a). The capacitance of the capacitor in terms of area and distance between the plates is,
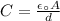
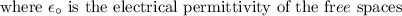
Substituting the known values,
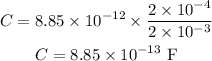
Thus, the value of the capacitanc is 8.85 times 10 power -13 Farad.
(b). The voltage across the battery is,
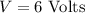
The charge stored in the capacitor in terms of the voltage and the capacitance is,
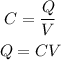
where Q is the charge stored in the capacitor
Substituting the known values,
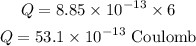
Thus, the charge stored in the parallel plate capacitor is 53.1 times 10 power -13 coulomb.