Problem:
A firefighter on the ground sees fire break through a window near the top of a building. The angle of elevation to the window seal is 28 degrees. The angle of elevation to the top of the building is 42 degrees. The firefighter is 75 ft from the building and her eyes are 5 feet above the ground. What Ruth window seal distance guess you report by radio to Firefighters on the roof?
Solution:
There are two big triangles, one of them is that formed by a fireman, the roof and the building foundation plus the height of the fireman as the vertices. So, the opposite side to the 42 degrees angle given is denoted by h_roof, and the adjacent side is 75 ft away from the building:
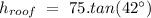
that is:
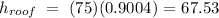
Now, the other big triangle is formed by the fireman, the window, and the building foundation plus the height of the fireman as vertices:

that is:
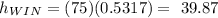
then, the difference between the heights is the roof-to-windowsill:
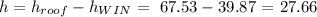
Then, we can conclude that the correct answer is:
