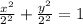Question

Which equation represents a circle? (x – 2)222+(y – 3)232=1 (x – 4)232+(y + k)212=1 x222+y222=1 x212+y232=1

Answer 1

Given:

Four different equations are given

Required:

To tell Which equation represents a circle?

Step-by-step explanation:

The formula for the equation of a circle is (x – h)2+ (y – k)2 = r2, where (h, k) represents the coordinates of the center of the circle, and r represents the radius of the circle. If a circle is tangent to the x-axis this means it touches the x-axis at that point

`\begin{gathered} (x^2)/(2^2)+(y^2)/(2^2)=1 \\ \\ x^2+y^2=2^2 \\ \\ so\text{ r =2} \end{gathered}`

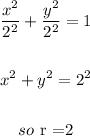
That is others are in the form of ellipse equation.

How do you find the general form of an ellipse?

The equation of an ellipse written in the form (x−h)2a2+(y−k)2b2=1. The center is (h,k) and the larger of a and b is the major radius and the smaller is the minor radius.

`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`

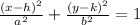
else three options resemble with ellipse equation

Required answer:

`(x^(2))/(2^(2))+(y^(2))/(2^(2))=1`