Question

If the line joining the points (a,4) and (2,-5) is parallel to the line with given equation 2x-3y=12 find the value of a

Answer 1

Parallel lines have the same slope, thus, using the equation of the parallel line, we can find out the slope of the line that passes through the given points.

To find the slope of a line given its equation, we have to put the equation into the slope-intercept form, whcih we can do by solving the equation for y:

`\begin{gathered} 2x-3y=12 \\ -3y=-2x+12 \\ y=(-2)/(-3)x+(12)/(-3) \\ y=(2)/(3)x-4 \end{gathered}`

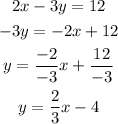
The slope of the line is the coefficient multiplying x, which is 2/3 in this case.

So, let's name the slope m:

`m=(2)/(3)`

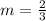
Since the lines are parallel, both have the same slope m.

Also, if we want to find the slope given two numbers on the line, we can use the following equation:

`m=(y_2-y_1)/(x_2-x_1)`

So, we have the points (a, 4) and (2, -5) and we have the slope m = 2/3. Substituting these, we have:

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1)_{} \\ (2)/(3)=(-5-4)/(2-a) \\ (2)/(3)=(-9)/(2-a) \\ 2(2-a)=3\cdot(-9) \\ 4-2a=-27 \\ -2a=-27-4 \\ -2a=-31 \\ a=(31)/(2) \end{gathered}`

Thus, the value of a is 31/2.