Question

Please help. I am not sure how to go about this.

Answer 1

(a) Given the functions:

`\begin{gathered} f(x)=x-4 \\ \\ g(x)=x+4 \end{gathered}`

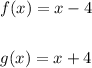
Then:

`\begin{gathered} f(g(x))=f(x+4) \\ \\ f(x+4)=x+4-4 \\ \\ f(g(x))=x \end{gathered}`

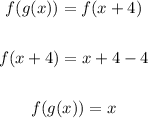
Similarly,

`\begin{gathered} g(f(x))=g(x-4) \\ \\ g(x-4)=x-4+4 \\ \\ g(f(x))=x \end{gathered}`

Two functions f and g are inverses of each other if and only if f(g(x))=x for every value of x in the domain of g and g(f(x))=x for every value of x in the domain of f.

ANSWER: f and g are inverse of each other.

(b) Given:

`\begin{gathered} f(x)=-(1)/(3x),x0 \\ \\ g(x)=(1)/(3x),x0 \end{gathered}`

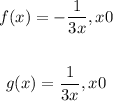
Then:

`\begin{gathered} f(g(x))=f((1)/(3x)) \\ \\ f((1)/(3x))=-(1)/(3((1)/(3x))) \\ \\ f(g(x))=-x \end{gathered}`

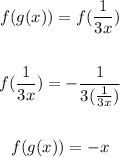
Also,

`\begin{gathered} g(f(x))=g(-(1)/(3x)) \\ \\ g(-(1)/(3x))=(1)/(3(-(1)/(3x))) \\ \\ g(f(x))=-x \end{gathered}`

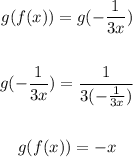
ANSWER: f and g are not inverses of each other.