Given:
The height equation is,
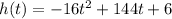
Step-by-step explanation:
For maximum/minimum of a function, the first derivative of function is 0.
Differentiate the function with respect to x.
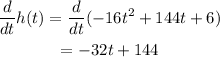
For maximum and minimum,
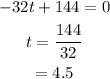
So rocket reach it maximum height after 4.5 seconds of launch.
Substitute 4.5 for t in the equation to determine the maximum reached by rocket.
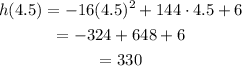
So maximum height of rocket is 330 feet.