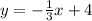The given equation is
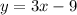
The new line is perpendicular to the given equation, which means we have to use the following formula.

Where the slope of the given line is 3 (the coefficient of x).
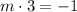
We solve for m.
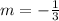
So, the slope of the new perpendicular line is -1/3.
According to the problem, the y-intercept of the new perpendicular line is 4. Now, we use the slope-intercept form to write the equation.

Therefore, the equation of the new line is