Question

Can someone please help me find the Answer to the following

Answer 1

First, to find the slant height, we use Pythagorean's Theorem to find the slant height, as the image below shows.

Then,

`\begin{gathered} h^2=10^2+7.5^2 \\ h^2=100+56.25 \\ h=\sqrt[]{156.25} \\ h=12.5ft \end{gathered}`

The slant height is 12.5 feet.

Now, the surface area formula is

`SA=2bs+b^2`

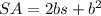
Where s = 12.5 and b = 15.

`\begin{gathered} SA=2\cdot15\cdot12.5+15^2 \\ SA=375+225 \\ SA=600ft^2 \end{gathered}`

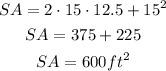
Hence, the surface area of the pyramid is 600 square feet.