Given the equation:
3x + 4y = -4
Let's graph the line that represents the equation above.
To grah the line, rewrite the equation in slope-intercet form:
y = mx + b
Where m is the slope and b is the y-intercept.
Rerite the equation for y:
3x + 4y = -4
Subtract 3x from both sides:
3x - 3x + 4y = -3x - 4
4y = -3x - 4
Divide all terms by 4:
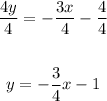
The slope of the line is -3/4, while the y-intercept is at (0, -1).
Now, let's graph the line using 3 points.
• When x = -4:
Substitute -4 for x and solve for y
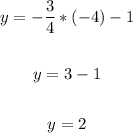
• When x = 0:
Substitute 0 for x and solve for y

• When x = 4:
Substitute 4 for x and solve for y

Therefore, we have the following points:
(-4, 2), (0, -1) and (4, -4)
Plot the three points on the graph, then connect all 3 points using a straight edge.
We have the graph attached below: