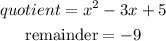Answer:
Quotient = x² - 3x + 5
Remainder = 9
Step-by-step explanation:
To make the synthetic division, we need to rewrite the dividend with all the degrees of the exponents, so:
x³ - 4x + 6 = x³ + 0x² - 4x + 6
Then, we will use the coefficient of each term: 1, 0, -4 and 6
On the other hand, the divisor should have the form (x - a), so:
x + 3 = x - (-3)
Therefore, a = -3, and we will use this number for the synthetic division.
Finally, the synthetic division is:
Where the first number goes down, then the blue -3 is calculated as the number as 1 x -3, and the yellow -3 is equal to the sum of the number numbers 0 and -3, so: 0 + (-3) = -3
In the same way, 9 = -3 x -3 and 5 = -4 + 9
Finally, -15 = 5 x -3 and -9 = 6 - 15
Now, the coefficients 1, -3, and 5 give us the quotient of the division, and -9 is the remainder. So, the solution of the division is: