Problem 7:
We determine the time as follows:
*We can proceed using the following expression:
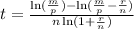
Here, t is the time it will take to pay, m is the maximum she can afford to pay each month, p is the base loan value, r is the interest rate, n is the number of periods. Now we replace:

So, she will take approximately 3.8 years to pay up the loan.
Problem 8:
We determine the time he has as follows:
We use the expression:
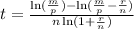
Here, t is the time it will take to pay, m is the maximum he can afford to pay each month, p is the base loan value, r is APR, n is the number of periods. Now we replace:
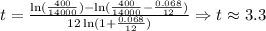
So, he will take approximately 3.3 years to pay the loan.
Problem 10:
We determine the amount he will have to pay as follows:
*We use the following expression:
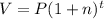
Here V is the value to obtain, P is the original amount, n is the interest rate and t is the number of periods, now we replace:
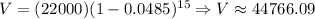
So, after 15 years he will have to pay approximately $44766.09.