SOLUTION
Let the time for the pipe to complete the Job be represented as

Let the time for the hose to complete the Job be represented as

The pipe and the hose completed the job in 3hours
Hence we have the equation
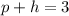
The inlet pipe alone can complete the job in one hour less time than the hose alone implies that
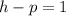
This leads to a system of equation which we now solve simultaneously
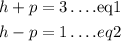
Adding eq1 and eq2, we o btain
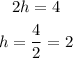
Substituting the value of h into eq1 we have
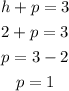
Therefore
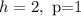
The time that the inlet pipe can complete the job alone is 1 hours
The time that the hose can complete the job alone is 2 hours