Answer:
14.6 m/s²
Step-by-step explanation:
First, we will make the free body diagram
Since the net vertical force is equal to 0 because the block is not moving up, we can write the following equation
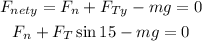
Then, we can solve for the normal force and replace Ft = 1197 N, m = 71 kg and g = 10 m/s²
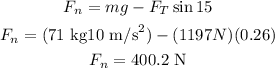
Now, we can write the following equation for the net horizontal force
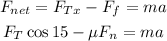
Where μ is the coefficient of friction and a is the acceleration of the block. Solving for a and replacing Ft = 1197 N, m = 71 kg, Fn = 400.2 N and μ = 0.3, we get

Therefore, the acceleration of the block is 14.6 m/s²