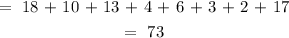Let Program 1, Program 2, and Program 3 be represented by P1, P2, and P3.
Given:
n(P1 n P2) = 6
n(P2 n P3) =8
n(P1 n P3) = 5
n(P1 n P2 n P3) = 2
n(P1 U P2' U P3') =18
n(P2) = 22
n(P3 U P1 U P2') = 16
n(P1 U P2 U P3)' = 17
Representing the information on a Venn diagram:
The number of people that were using Program 2 but not Program 3:
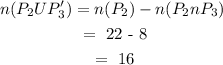
Number of people surveyed
The number of people surveyed is the sum of the individual subsets: