Question

Solve for x in the equation x2+2x+ 1 = 17.X=-1+ /15X=-1+ /17X=-2+2.15X=-1+ /13

Answer 1

First, write the quadratic equation in standard form. Then, use the quadratic formula to find the solutions for the quadratic equation.

Remember that if a quadratic equation is written in standard form:

`ax^2+bx+c=0`

Where a, b and c are constants, then the solutions for x are given by:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Starting with the given equation:

`x^2+2x+1=17`

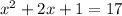
Substract 17 from both members to write the equation in standard form:

`\begin{gathered} \Rightarrow x^2+2x+1-17=17-17 \\ \Rightarrow x^2+2x-16=0 \end{gathered}`

Use the quadratic formula, setting a=1, b=2 and c=-16:

`\begin{gathered} x=\frac{-(2)\pm\sqrt[]{(2)^2-4(1)(-16)}}{2(1)} \\ =\frac{-2\pm\sqrt[]{4+64}}{2} \\ =\frac{-2\pm\sqrt[]{68}}{2} \end{gathered}`

Simplify the expression using the properties of radicals. Since 68 is equal to 4 times 17, then:

`\begin{gathered} x=\frac{-2\pm\sqrt[]{68}}{2} \\ =\frac{-2\pm\sqrt[]{4\cdot17}}{2} \\ =\frac{-2\pm\sqrt[]{4}\cdot\sqrt[]{17}}{2} \\ =\frac{-2\pm2\cdot\sqrt[]{17}}{2} \\ =\frac{2(-1\pm\sqrt[]{17})}{2} \\ =-1\pm\sqrt[]{17} \end{gathered}`

Therefore, the solutions for x in the given equation are:

`\begin{gathered} x_1=-1+\sqrt[]{17} \\ x_2=-1-\sqrt[]{17} \end{gathered}`