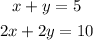Question

How do u find weather the system has one solution,no solutiin,solution,infinitely many solutions

Answer 1

1st case: the system has one solution

For example:

Given this system:

`\begin{gathered} x+y=5 \\ 2x-y=4 \\ \text{Let:} \\ x+y=5\text{ (1)} \\ 2x-y=4\text{ (2)} \\ \text{ Using elimination method:} \\ (1)+(2)\colon \\ x+2x+y-y=9 \\ 3x=9 \\ x=(9)/(3) \\ x=3 \\ y=5-x \\ y=5-3 \\ y=2 \end{gathered}`

graphically, a system has a solution if the two lines intersect, the point of intersection is the solution.

--------------------------------------------

2nd case: the system has no solution

A system has no solution, when the lines are parallel and have different intercepts, for example:

`\begin{gathered} y=2x+1 \\ y=2x-3 \end{gathered}`

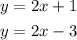
as you can see the lines never cross each other.

3rd case: the system has infinitely many solutions ​

occurs when one line is a scalar multiple of the other, in other words it is the same line. for example:

`\begin{gathered} x+y=5 \\ 2x+2y=10 \end{gathered}`