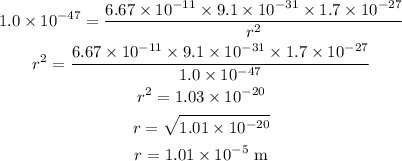Question

3. The mass of an electron is 9.1x10^-31 kg. The mass of a proton is 1.7x10^-27 kg.The gravitational force between them in the hydrogen atom is 1.0x10^-47 N.What is the separation distance between them?

Answer 1

Given:

The mass of the electron is,

`m_e=9.1*10^(-31)\text{ kg}`

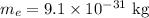
The mass of the proton is,

`m_p=1.7*10^(-27)\text{ kg}`

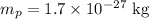
The gravitational force between the electron and the proton in the hydrogen atom is,

`1.0*10^(-47)\text{ N}`

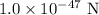
To find:

the separation between them

Step-by-step explanation:

The gravitational force between two masses is,

`F=(Gm_1m_2)/(r^2)`

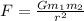
Here, the universal gravitational constant is,

`G=6.67*10^(-11)\text{ Nm}^2kg^(-2)`

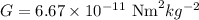
Substituting the values we get,

`\begin{gathered} 1.0*10^(-47)=(6.67*10^(-11)*9.1*10^(-31)*1.7*10^(-27))/(r^2) \\ r^2=(6.67*10^(-11)*9.1*10^(-31)*1.7*10^(-27))/(1.0*10^(-47)) \\ r^2=1.03*10^(-20) \\ r=\sqrt{1.01*10^(-20)} \\ r=1.01*10^(-5)\text{ m} \end{gathered}`