Question

Convert the repeated decimal 0.47 into a fraction using infinite geometric series.

Answer 1

47/99

Step-by-step explanation:

Given the repeated decimal 0.4747...

This can be splitted into;

0.47 + 0.0047 + 0.000047 + ...

On rewriting;

47/100 + 47/10000 + 47/1000000 + ...

The given series is a geometric progression

The sum to infinity of a geometric progression is expressed as;

`S\infty\text{ = }(a)/(1-r)`

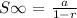
a is the first term

r is the common ratio

From the sequence;

a = 47/100

r = (47/10000)/(47/100)

r = 47/10000 * 100/47

r = 1/100

Substitute;

`\begin{gathered} S\infty\text{ = }((47)/(100))/(1-(1)/(100)) \\ S\infty\text{ = }((47)/(100))/((99)/(100)) \\ S\infty\text{ = }(47)/(100)\cdot(100)/(99) \\ S\infty\text{ = }(47)/(99) \end{gathered}`

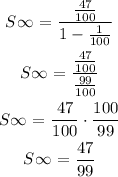
Henec the repeated fraction to decimal is 47/99