we have the equation
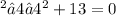
Group similar terms and move the constant to the right side
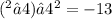
Complete the square
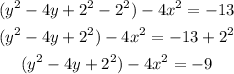
Rewrite as a perfect square
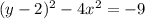
Divide both sides by -9
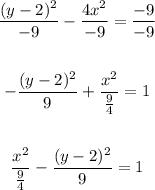
The coordinates of the center are (0,2)
The transverse axis is on the x-axis
a^2=9/4 -----------> a=3/2
b^2=9 -----------> b=3
The vertices are --------> (0+1.5,2) and (0-1.5,2)
so
Vertices at (1.5,2) and (-1.5,2)
Find out the value of c
c^2=a^2+b^2
c^2=(9/4)+9
c^2=45/9
c=√5
Find out the coordinates of the foci
(0+√5,2) and (0-√5,2)
using a graphing tool
The domain is the interval (-infinite, -1.5) U (1.5, infinite)
The range is the interval (-infinite, infinite)