The function given is:
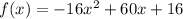 PART A
PART AThe factorization steps are shown below:
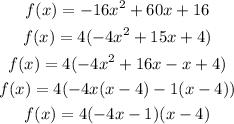 PART B
PART BTo find the x intercepts, we set f(x) equal to 0 and solve for x:
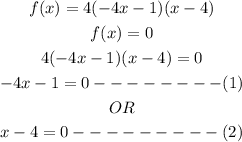
Solving (1), we have:
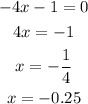
and, solving (2), we have:
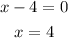
The x-intercepts are
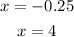 PART C
PART CThe standard equation of a quadratic is

The parabola opens upward when a is positive and opens downward when a is negative
1. When parabola opens upward, the end behavior can be described as:
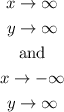
2. When parabola opens downward, the end behavior can be described as:
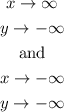
Our equation has an "a" value that is negative! So, the parabola opens downward and the end behvaior can be described as:
As x goes to infinity (gets infinitely large), y goes to negative infinity (gets infinitely small) and as x goes to negative infinity (gets infinitely small), y goes to negative infinity (get infinitely small).
PART DIn Part B, we found the x-intercepts. Those are the x-axis cutting points. We can draw those first.
Then,
Using the end behavior information that we found in Part C, we can draw the parabola. The rough sketch is shown:
The exact graph is shown below, for reference: