Question

Write an equation for the conic in the xy-plane for

Answer 1

Given:

`((x^(\prime))^2)/(15)-((y^(\prime))^2)/(6)=1\text{ at }\theta=30^o`

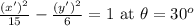
To find:

We need to find an equation for the conic in the xy-plane.

Step-by-step explanation:

We can find the conic equation by using the following equation.

`x^(\prime)=x\cos \theta+y\sin \theta\text{ and }y^(\prime)=y\cos \theta-x\sin \theta`
`\text{Substitute }\theta=30^o\text{ in the eqatuions.}`

`x^(\prime)=x\cos 30^o+y\sin 30^o\text{ and }y^(\prime)=y\cos 30^o-x\sin 30^o\text{.}`
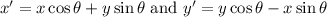
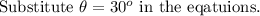
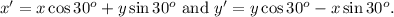
`\text{Use }\cos 30^o=\frac{\sqrt[]{3}}{2}\text{ and }\sin 30^o=(1)/(2)\text{.}`

`x^(\prime)=x(\frac{\sqrt[]{3}}{2})+y((1)/(2))\text{ and }y^(\prime)=y(\frac{\sqrt[]{3}}{2})-x((1)/(2))`

`x^(\prime)=\frac{\sqrt[]{3}}{2}x+(1)/(2)y\text{ and }y^(\prime)=\frac{\sqrt[]{3}}{2}y-(1)/(2)x`

`\text{ Substitute }x^(\prime)=\frac{\sqrt[]{3}}{2}x+(1)/(2)y\text{ and }y^(\prime)=\frac{\sqrt[]{3}}{2}y-(1)/(2)x\text{ in the given equation.}`

`\frac{(\frac{\sqrt[]{3}}{2}x+(1)/(2)y)^2}{15}-\frac{(\frac{\sqrt[]{3}}{2}y-(1)/(2)x)^2}{6}=1`

`(1)/(15)(\frac{\sqrt[]{3}}{2}x+(1)/(2)y)^2-(1)/(6)(\frac{\sqrt[]{3}}{2}y-(1)/(2)x)^2=1`

`(1)/(15)\mleft\lbrace(\frac{\sqrt[]{3}x}{2})^2+(2*\frac{\sqrt[]{3}x}{2}*(y)/(2))+((y)/(2))^2\mright\rbrace-(1)/(6)\mleft\lbrace(\frac{\sqrt[]{3}y}{2})^2-2*\frac{\sqrt[]{3}y}{2}*(x)/(2)+((x)/(2))^2\mright\rbrace=1`

`(1)/(15)\mleft\lbrace(3x)/(4)^2+\frac{\sqrt[]{3}xy}{2}+(y^2)/(4)^{}\mright\rbrace-(1)/(6)\mleft\lbrace(3y)/(4)^2-\frac{\sqrt[]{3}xy}{2}+(x)/(4)^2\mright\rbrace=1`

`(3x^2)/(15*4)^{}+\frac{\sqrt[]{3}xy}{15*2}+(y^2)/(15*4)^{}-(3y^2)/(6*4)^{}+\frac{\sqrt[]{3}xy}{6*2}-(x)/(6*4)^2=1`

`(x^2)/(20)^{}+\frac{\sqrt[]{3}xy}{30}+(y^2)/(60)^{}-(y^2)/(8)^{}+\frac{\sqrt[]{3}xy}{12}-(x^2)/(24)^{}=1`

Here LCM is 360, making the denominator 360.

`18x^2+12\sqrt[]{3}xy+6y^2-45y^2+30\sqrt[]{3}xy-15x^2=360`

`3x^2+42\sqrt[]{3}xy-39y^2-360=0`

Final answer:

The equation for the conic in the xy-plane is

`3x^2+42\sqrt[]{3}xy-39y^2-360=0`