Question

Use systems to solve :The length of a rectangle is 2 cm more than itswidth. If the perimeter is 52 cm, find the width.

Answer 1

The width is 12 cm

Step-by-step explanation

The length L of the rectangle is 2 cm more than its width W. With this we have one equation:

`L=W+2`

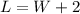
Then the perimeter is 52cm, which is the sum of the sides of the rectangle:

`P=W+W+L+L=2W+2L`

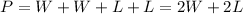
Therefore the system to solve is:

`\begin{cases}L=W+2 \\ 52=2W+2L\end{cases}`

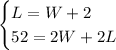
Using the substitution method we can solve just for W. Replace L in the second equation by its value in terms of W from the first equation:

`52=2W+2(W+2)`

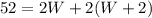
Use the distributive property to eliminate the parenthesis:

`52=2W+2W+4`

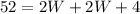
Add like terms:

`52=4W+4`

And solve for W:

`\begin{gathered} 4W=52-4 \\ 4W=48 \\ W=(48)/(4) \\ W=12 \end{gathered}`

Therefore, the width of the rectangle is 12cm