Question

Need help with example #4 Find all missing angles and sides.

Answer 1

We will use the law of sines and law of cosines shown below

`\begin{gathered} c=√(a^2+b^2-2ab\cos C)\rightarrow\text{ law of cosines} \\ and \\ (sinA)/(a)=(sinB)/(b)=(sinC)/(c)\rightarrow\text{ law of sines} \end{gathered}`

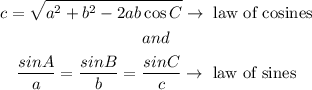
Therefore, in our case, finding side c.,

`\begin{gathered} a=28,b=13,C=49\degree \\ \Rightarrow c=√(784+169-2*28*13cos(49\degree)) \\ \Rightarrow c\approx21.8 \end{gathered}`

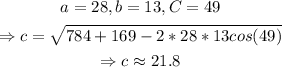
Thus, side c is approximately 21.8km.

Finding the missing angles using the law of sines,

`\begin{gathered} A=\cos^(-1)((c^2+b^2-a^2)/(2bc)) \\ \Rightarrow A=\cos^(-1)((21.8^2+13^2-28^2)/(2*13*21.8)) \\ \Rightarrow A\approx104.3 \\ \end{gathered}`

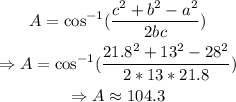
Similarly, in the case of angle B,

`sinB=(13)/(21.8)sin(49\degree)\approx26.7\degree`

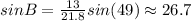
Therefore, the answers are

c=21.8km,