Write an equation in general form of the circle with the given properties.
Ends of diameter at (5,7) and (-5,-7)
we have that
the equation of the circle is
(x-h)^2+(y-k)^2=r^2
where (h,k) is the center and r is the radius
step 1
Find the center
Remember that
The center of the circle is the midpoint of diameter
so
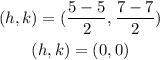
the center is the origin
step 2
Find the radius
Find the diameter
calculate the distance between two points
![\begin{gathered} d=\sqrt[\square]{(-7-7)^2+(-5-5)^2} \\ d=\sqrt[\square]{(-14)^2+(-10)^2} \\ d=\sqrt[\square]{296} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/tphepxfmb6zebgn8b31ybkuqnf39skot1b.png)
simplify
![D=\sqrt[\square]{296}=2\sqrt[\square]{74}](https://img.qammunity.org/2023/formulas/mathematics/college/tbmdaqhucwvt9b5ew1bn112oztayhxk0jd.png)
the radius is half the diameter
so
r=2√74/2=√74
step 3
the equation iof the circle is
x^2+y^2=(√74)^2
x^2+y^2=74