SOLUTION
The price of the car = $12,000
The depreciate by 10%
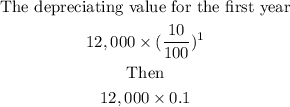
Then
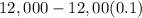
Then
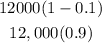
For the first year the depreciating value will be
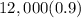
Base on the number of years, the exponential equation will be
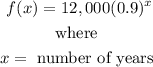
Therefore
The exponential equation that represent the value of the car is
F(x)=12,000(0.9)^x
The price of the car in 5 yeras will be obtain by substituting x=5 into the equation above
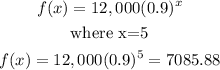
The car will worth $7085.88 after 5 years
Similarly, The for 12 years we have x=12
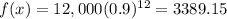
The car will worth $3389.15 after 12 years