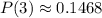Question

If a seed is planted, it has a 80% chance of growing into a healthy plant. If 8 seeds are planted, what is the probability that exactly 3 don't grow?

Answer 1

Given that a seed that is planted has an 80% chance of growing into a healthy plant, and knowing that you have to find the probability that exactly 3 seeds of 8 seeds planted don't grow, you need to use this Binomial Distribution Formula:

`P(x)=(n!)/((n-x)!x!)\cdot p^x(1-p)^(n-x)`

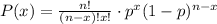
Where "n" is the number of trials, "x" is the number of successes desired, and "p" is the probability of getting a success in one trial.

In this case, you can identify that:

`p=100\text{\%}-80\text{\%}=20\text{\%}=0.20`
`\begin{gathered} n=8 \\ x=3 \end{gathered}`

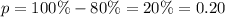
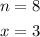
Now you can substitute values into the formula and evaluate:

`P(3)=((8!)/((8-3)!3!))(0.20)^3(1-0.20)^(8-3)`
`P(3)=(57344)/(390625)\approx0.1468`

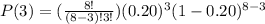
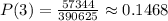
Hence, the answer is:

`P(3)\approx0.1468`