Question

The area of a soccer field is ( 24x^2 + 100x + 100) m^2. The width of the field is (4x + 10)m. What is the length?Please help, need right away.Be sure to show work. NEED HELP BEEN ON THIS PROBLEM FOR 2 DAYS

Answer 1

hello

to solve this question, we have to understand that a soccer field is rectangular in shape and we can find this length from factoring the area

formula of area of a rectangle

`\begin{gathered} A=L* W \\ A=\text{area} \\ L=\text{length} \\ W=\text{width} \end{gathered}`
`\begin{gathered} A=24x^2+100x+100 \\ W=4x+10 \\ L=\text{ ?} \end{gathered}`

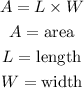
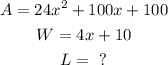
we can proceed to solve this by dividing the polynomial or simply checking it from the options

from the options given,

we have option A

3x + 10

let's multiply both the L and W to see if it gives us the answer

`(4x+10)*(3x+10)=12x^2+70x+100_{}`

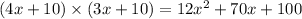
option A is incorrect

let's test for option B

L= 6x + 10

`\begin{gathered} A=L* W \\ (6x+10)*(4x+10)=24x^2+100x+100_{} \end{gathered}`

option B is correct

let's test for option C

L= 6x + 1

`\begin{gathered} A=L* W \\ (6x+1)*(4x+10)=24x^2+70x+10 \end{gathered}`

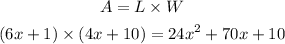
option C is also incorrect and so it'll be for option D

from the calculations above, only option B corresponds with the value of length for the soccer field