Question

The question is in the picture. Using the answer choice word bank, fill in the proportion to find the volume of the larger figure.

Answer 1

It is given that two similar solids have surface areas of 48 m² and 147 m², and the smaller solid has a volume of 34 m³.

It is required to find the volume of the larger solid.

Recall that the if the scale factor of similar solids is a/b, then the ratio of their areas is the square of the scale factor:

`\frac{\text{ Area of smaller solid}}{\text{ Area of larger solid}}=(a^2)/(b^2)`

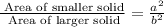
Substitute the given areas into the equation:

`(48)/(147)=(a^2)/(b^2)`

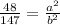
Find the scale factor a/b:

`\begin{gathered} \text{ Swap the sides of the equation:} \\ \Rightarrow(a^2)/(b^2)=(48)/(147) \\ \text{ Reduce the fraction on the right with }3: \\ \Rightarrow(a^2)/(b^2)=(16)/(49) \\ \text{ Take the square root of both sides:} \\ \Rightarrow(a)/(b)=(4)/(7) \end{gathered}`

Recall that if the scale factor of two similar solids is a/b, then the ratio of their volumes is the cube of the scale factor:

`\frac{\text{ Volume of smaller solid}}{\text{ Volume of larger solid}}=\left((a)/(b)\right)^3`

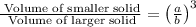
Let the volume of the larger solid be V and substitute the given value for the volume of the smaller solid:

`(34)/(V)=\left((a)/(b)\right)^3`

Substitute a/b=4/7 into the proportion:

`\begin{gathered} (34)/(V)=\left((4)/(7)\right)^3 \\ \\ \Rightarrow(34)/(V)=(4^3)/(7^3) \\ \\ \Rightarrow(34)/(V)=(64)/(343) \end{gathered}`

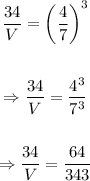
Find the value of V in the resulting proportion:

`\begin{gathered} \text{ Cross multiply:} \\ 64V=343\cdot34 \\ \text{ Divide both sides by }64: \\ \Rightarrow(64V)/(64)=(343\cdot34)/(64) \\ \Rightarrow V\approx182.22\text{ m}^3 \end{gathered}`

Answers:

The required proportion is 34/V =64/343.

The volume of the larger solid is about 182.22 m³.