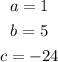Given the general expression of a quadratic function,
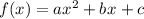
The given function is,
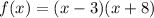
Expanding the right-hand side of the equation
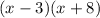
Apply FOIL method:
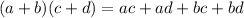
Therefore,
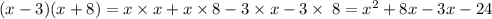
Simplify
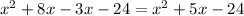
Therefore, the function in standard form is
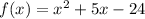
Now, comparing the general quadratic function and the function given.
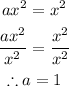
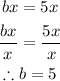
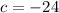
Hence, the answers are