Question

Please explain why the lowest value is at four why it’s not at six?

Answer 1

- The lowest value of the sinusoidal function is usually gotten using the formula:

`\begin{gathered} L=M-A \\ where, \\ M=\text{ The value of the midline} \\ A=\text{ The Amplitude or highest value} \end{gathered}`

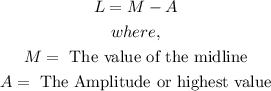
- The question says that the sea falls 6ft below sea level and rises 6ft above sea level.

- The midline M represents the sea level and the rise of 6ft represents the amplitude.

- Thus, the above equation can be rewritten as:

`L=M-6`

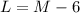
- The formula for finding the peak of the sinusoidal is:

`\begin{gathered} U=M+A \\ where, \\ U=\text{ The Peak or height of the water} \end{gathered}`

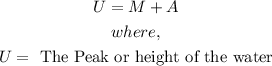
- We can similarly rewrite the equation as:

`U=M+6`

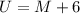
- We have been given the peak height of the water to be 16. Thus, U = 16. Thus, we can find the midline (M) as follows:

`\begin{gathered} U=M+6 \\ put\text{ }U=16 \\ 16=M+6 \\ \text{ Subtract 6 from both sides} \\ M=16-6=10 \end{gathered}`

- Thus, the midline (M) is at 10ft. This also implies that the sea level is at 10 ft.

- Thus, we can find the lowest value or low line as follows:

`\begin{gathered} L=M-6 \\ \text{ We know that }M=10 \\ \\ \therefore L=10-6=4ft \end{gathered}`

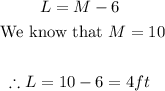
Final Answer

The lowest value or Low line is at 4ft